Μόνο το 2% των ανθρώπων μπορεί να λύσει αυτό το τεστ IQ – πρόβλημα, σύμφωνα με καθηγητή μαθηματικών
Tο τεστ είναι ένα γεωμετρικό παζλ, Η γεωμετρία είναι ο κλάδος των μαθηματικών που ασχολείται με το σχήμα μεμονωμένων αντικειμένων, τις χωρικές σχέσεις μεταξύ διαφόρων αντικειμένων και τις ιδιότητες του περιβάλλοντος χώρου. Η Britannica εξηγεί ότι η γεωμετρία είναι ένας από τους παλαιότερους κλάδους των μαθηματικών, καθώς προέκυψε ως απάντηση σε πρακτικά προβλήματα όπως αυτά που συναντάμε στην τοπογραφία, και το όνομά της προέρχεται από ελληνικές λέξεις που σημαίνουν «μέτρηση της γης».
Ένας καθηγητής μαθηματικών μοιράστηκε μια γρίφο στα social media και ισχυρίστηκε ότι μόνο το 2% των ανθρώπων μπορεί να τον λύσει. Ο γρίφος ξεκινά με μια εικόνα από ένα μικρό τρίγωνο μέσα σε ένα μεγαλύτερο τρίγωνο, με δύο δεδομένα δηλαδή τις γωνίες, 20° και 80°.
Ο καθηγητής, με το όνομα «Professor_1o1math» στο Facebook, πρότεινε στους θεατές να προσπαθήσουν να βρουν τη λύση πριν αποκαλύψει την απάντηση σε βίντεο. Εξήγησε ότι το πρόβλημα απαιτεί απλή γεωμετρία, αλλά ότι μπορεί να είναι δύσκολο. Ο στόχος είναι να υπολογιστεί μια γωνία στο μικρότερο τρίγωνο.
Τεστ IQ: Μόνο το 2% των ανθρώπων μπορεί να υπολογίσει τις γωνίες αυτού του τριγώνου
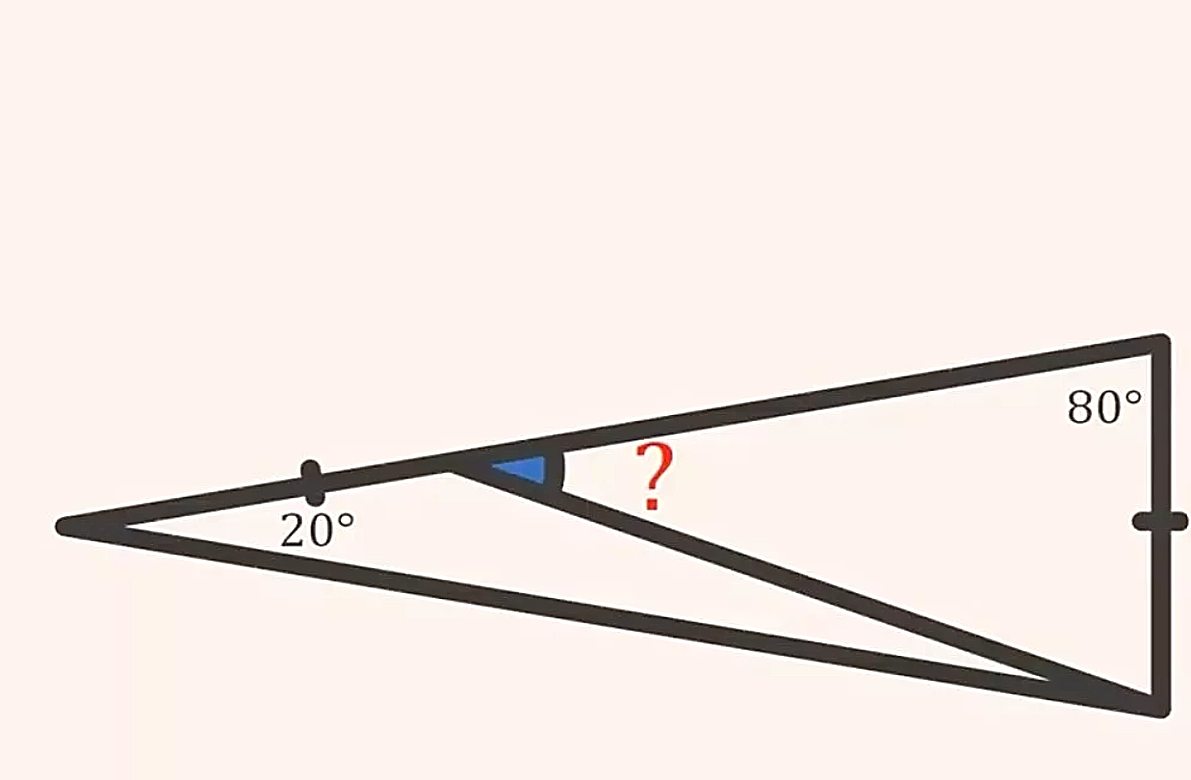
Λύση
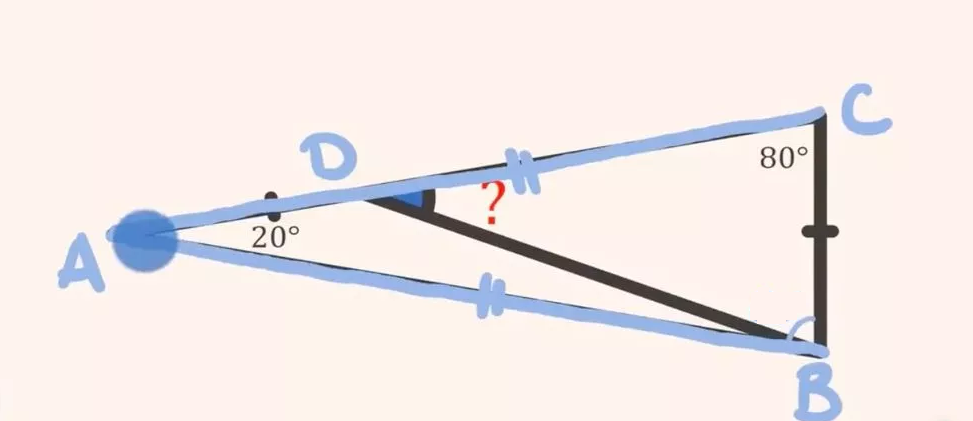
Για να λύσουμε το πρόβλημα, ο καθηγητής εξηγεί ότι πρέπει να εντοπίσουμε τις γωνίες βήμα προς βήμα. Αρχικά ονόμασε τις γωνίες ως A, B, C, D.
Βήμα 1: Βρείτε τη γωνία B
Το άθροισμα των γωνιών σε οποιοδήποτε τρίγωνο είναι 180°. Επομένως, η γωνία B (κάτω δεξιά) υπολογίζεται ως εξής: 180° − 80° − 20° = 80°. Άρα αφού η γωνία B και η γωνία C είναι και οι δύο 80° τότε το τρίγωνο είναι ισοσκελές.
Βήμα 2: Προσθήκη Ισοπλεύρου τριγώνου
Το επόμενο βήμα είναι να προσθέσουμε ένα ισόπλευρο τρίγωνο πάνω από το αρχικό τρίγωνο με βάση την πλευρά ΑΒ. Ένα ισόπλευρο τρίγωνο έχει όλες τις γωνίες 60°. Αυτή η προσθήκη εισάγει μια νέα γωνία, τη γωνία E, η οποία είναι 60°.
Βήμα 3: Υπολογισμός Γειτονικών Γωνιών
Τώρα, μπορούμε να υπολογίσουμε τη νέα γειτονική γωνία. Δεδομένου ότι η συνολική γωνία είναι 60° και η μικρότερη γωνία είναι 20°, η υπόλοιπη γωνία γίνεται: 60° − 20° = 40°
Βήμα 4: Βρείτε τις Γωνίες E, B, C
Τώρα πρέπει να υπολογίσουμε τη γωνία που σχηματίζεται από τις γωνίες E, B και C. Δεδομένου ότι η γωνία B και η γωνία C είναι και οι δύο 80° και η γωνία στο ισόπλευρο τρίγωνο είναι 60°, μπορούμε να βρούμε τη γωνία E, B, C ως εξής: 80° − 60° = 20°
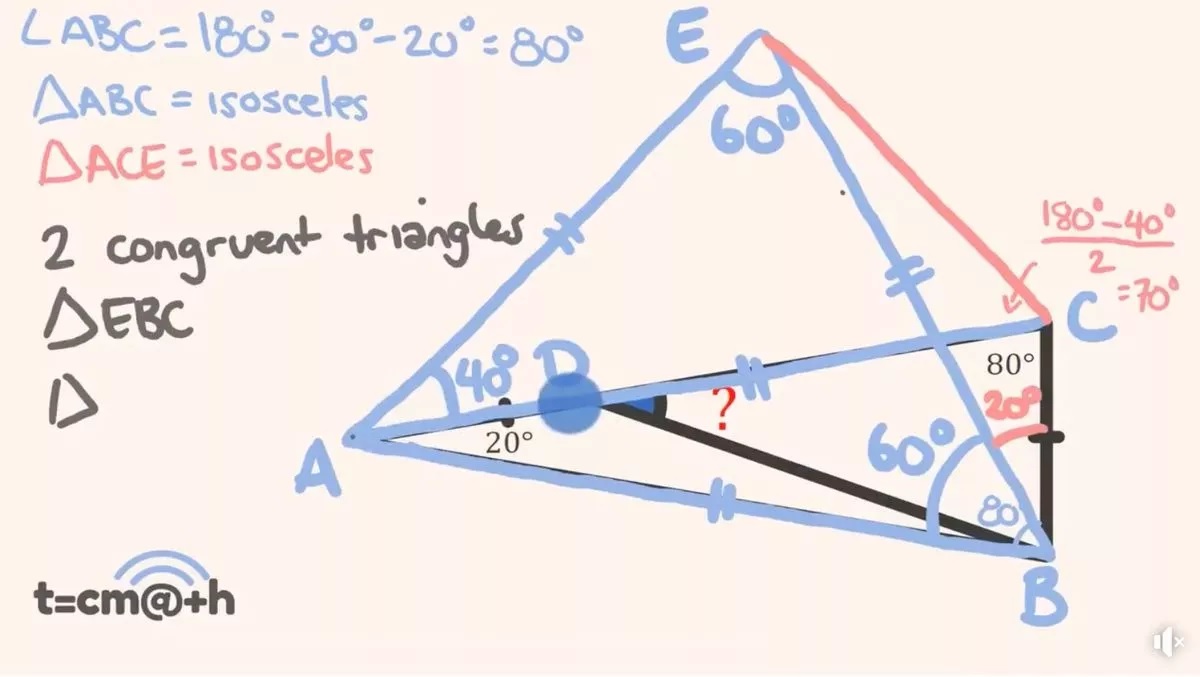
Τελικό Βήμα: Δημιουργία νέου τριγώνου
Τέλος, σχεδιάζουμε μια γραμμή μεταξύ των σημείων C και E, σχηματίζοντας ένα νέο τρίγωνο AEC. Αυτό το τρίγωνο είναι επίσης ισοσκελές, καθώς οι πλευρές AC και ΑΕ είναι ίσες. Στο νέο τρίγωνο AEC, αφού η γωνία Α είναι 40° τότε οι άλλες γωνίες είναι 70° καθώς, 70° + 70° + 40° = 180°.
Ο καθηγητής εξηγεί ότι σχεδιάζοντας τα πρόσθετα τρίγωνα, θα έχετε σχεδιάσει δύο όμοια τρίγωνα. Τα δύο τρίγωνα λέγεται ότι είναι συγγενή αν οι πλευρές τους έχουν το ίδιο μήκος και οι γωνίες τους έχουν το ίδιο μέτρο. Αυτό σημαίνει ότι δύο τρίγωνα μπορούν να τοποθετηθούν πάνω σε δύο πλευρές και γωνίες.
Συνεχίζοντας την εξήγησή του, ο καθηγητής υποδεικνύει δύο από τα τρίγωνα EBC και BAD είναι πανομοιότυπα. Στη συνέχεια πρόσθεσε τις 80° και τις 70°, τις οποίες υπολογίσαμε προηγουμένως, και προσθέτει συνολικά 150°.
Αυτό μας φέρνει στη λύση του προβλήματος, καθώς ο υπολογισμός της μικρότερης γωνίας που ψάχναμε λειτουργεί ως εξής. Μία ευθεία είναι επί της ουσίας μία γωνία 180°. Άρα αφαιρονται τις 150°, έχουμε την απάντηση που είναι 30°.









Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου